公平组合游戏(Impartial Game)的定义如下:
- 游戏有两个人参与,二者轮流做出决策,双方均知道游戏的完整信息;
- 任意一个游戏者在某一确定状态可以作出的决策集合只与当前的状态有关,而与游戏者无关;
- 游戏中的同一个状态不可能多次抵达,游戏以玩家无法行动为结束,且游戏一定会在有限步后以非平局结束。
n 堆物品,第 i 堆物品中含有 ai 个物品。
两位玩家轮流操作,每次可以取走任意一堆的任意个物品,但不能不取。
取走最后一个物品的人获胜(败者面临了一个无法行动的状态)。
Nim 游戏是一个经典的公平组合游戏,接下来的讲解会以此为例。
显然我们可以把每种可能的游戏局面称为一个状态,并抽象为图中的点,如果由一个状态可以通过一次操作转换到另一个状态,就给这两个抽象点之间连上一条有向边。
这样一个公平组合游戏就可以抽象为一个博弈图(后面所说的博弈图都指公平组合游戏的博弈图),显然根据公平组合游戏的特点,可以知道博弈图是一个有向无环图(DAG)。
比如下面就是初始局面为 a={1,2} 的 Nim 游戏对应的博弈图。
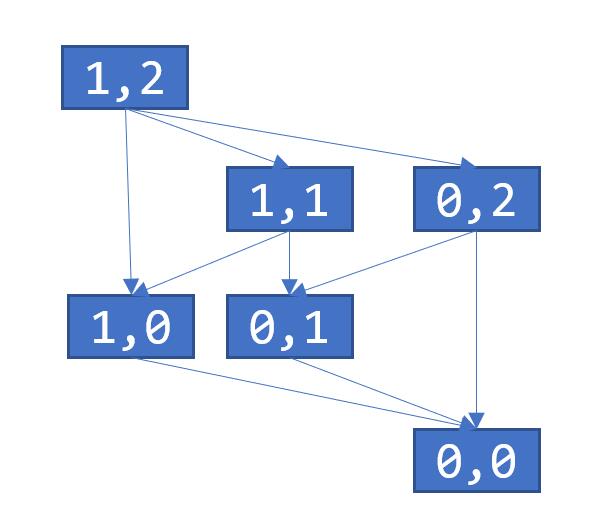
根据 Nim 游戏的特点很容易知道:
- 出度为 0 的状态都是先手必败态(以下简称必败态)
- 如果某个状态的后继状态存在必败态,那么这个状态就是先手必胜态(以下简称必胜态)
- 如果某个状态的后继状态都是必胜态,那么这个状态就是必败态
定义 Nim 和=a1⊕a2⊕⋯⊕on(⊕ 表示异或和)
那么有 Nim 和 为 0 的 Nim 游戏为先手必败的,否则为先手必胜的。
显然有:
- 对于一个 Nim 和 非 0 的局面,可以通过操作转变为 Nim 和 为 0 的局面。
- 对于一个 Nim 和 为 0 的局面,无法通过操作转变为 Nim 和 为 0 的局面。
- 最终局面 a1=a2=⋯=an=0 为必败态,Nim 和 为 0。
那么对于一个 Nim 和 非 0 的局面,先手可以永远让后手面临 Nim 和 为 0 的状态,而自己永远处于 Nim 和 非 0 的状态。所以先手是必胜的。
那么对于一个 Nim 和 为 0 的局面,先手只能给后手一个 Nim 和 非 0 的状态,而后手总能再次把 Nim 和 调整为 0 后给先手去面对。所以先手是必败的。
有向图游戏是一个经典的博弈游戏——实际上,大部分的公平组合游戏都可以转换为有向图游戏。
在一个有向无环图中,只有一个起点,上面有一个棋子,两个玩家轮流沿着有向边推动棋子,不能走的玩家判负。
如果对于状态 x:
- 如果 x 没有后续状态,我们就定义 SG(x)=0
- 如果 x 有 k 个后续状态 y1,y2,…,yk,那么就定义 SG(x)=mex{SG(y1),SG(y2),…,SG(yk)}.
- mex{…} 表示中括号中没出现的最小的自然数
- mex{1,2,3}=0
- mex{0,1,2,5}=3
实际上,SG 函数告诉我们的信息是:
- 如果 SG(x)=0,那么 x 是一个必败态(不能进一步转换了)。
- 如果 SG(x)=n, (n>0),那么 x 操作后必然可以抵达 ”SG 值为 0∼n−1 中任意一种“的状态,且有可能可以抵达”SG 值大于n“的状态
- 这就相当于 Nim 中的一堆石子了,这堆石子如果有 n 个,可以在一次操作后变为 0∼n−1 个。变多的可能性可以不用在意,因为另一个玩家可以再次变小到为 n,后续会详细描述。
对于 n 个有向图游戏,如果起点分别为 s1,s2,…,sn。
那么当 SG(s1)⊕SG(s2)⊕⋯⊕SG(sn)=0 时为先手必败态。否则为先手必胜态。
且这 n 个有向图游戏可以归纳为一个 SG 函数值为 SG(s1)⊕SG(s2)⊕⋯⊕SG(sn) 的有向图游戏。
- 最终的必败态为所有游戏都必败时的状态,那时所有 SG 函数的异或和为 0.
- 对于 SG(s1)⊕SG(s2)⊕⋯⊕SG(sn)=0 的游戏。
- 如果先手将某个游戏对应的 SG 值变大了,那么显然后手可以将其调整回原本的 SG 值。
- 所以先手想要有变化,只能把某个 SG(si) 变为 0∼SG(si)−1 中的某个 SG 值,这会让后手得到一个异或和非 0 的状态。
- 对于 SG(s1)⊕SG(s2)⊕⋯⊕SG(sn)=0 的游戏,根据 SG 函数的性质,先手可以操作其中的某个游戏,使得 SG(s1)⊕SG(s2)⊕⋯⊕SG(sn)=0,这会让后手永远面临异或和为 0 的状态。
所以,类似于 Nim 游戏,我们有了 SG 定理
https://zhuanlan.zhihu.com/p/437746506
