¶ 二分查找
¶ 循环控制(必须要掌握)
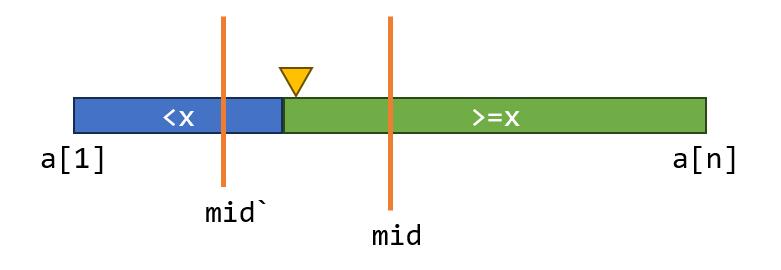
//在有序的 a[1]~a[n] 中找到第一个大于等于 x 的位置
int l = 1;
int r = n;
int ans = n + 1;
while (l <= r)
{
int mid = (l + r) / 2;
if (a[mid] >= x)
{
ans = mid;
r = mid - 1;
}
else
l = mid + 1;
}
¶ STL 的二分三兄弟
使用前必须保证数组按小于号从小到大有序!
int n, a[1123456];lower_bound(a + 1, a + n + 1, x)返回第一个大于等于x的位置(指针/迭代器)lower_bound(a + 1, a + n + 1, x) - a可以得到对应的下标。- 如果找不到,会返回最后一个位置的后一个位置,即
a + n + 1。
upper_bound(a + 1, a + n + 1, x)返回第一个大于x的位置(指针/迭代器)upper_bound(a + 1, a + n + 1, x) - a可以得到对应的下标。- 如果找不到,会返回最后一个位置的后一个位置,即
a + n + 1。
binary_search(a + 1, a + n + 1, x)返回一个布尔值,表示能否查找到x
vector<int> a;lower_bound(a.begin(), a.end(), x)lower_bound(a.begin(), a.end(), x) - a.begin()可以得到对应的下标。- 如果找不到,会返回最后一个位置的后一个位置,即
a.end()。
upper_bound(a.begin(), a.end(), x)upper_bound(a.begin(), a.end(), x) - a.begin()可以得到对应的下标。- 如果找不到,会返回最后一个位置的后一个位置,即
a.end()。
binary_search(a.begin(), a.end(), x)- 如果找不到,会返回
a.end()
注意:如果是从大到小有序的序列,查找第一个小于 x 的元素,那么需要指定第四个参数
小技巧:显然 upper_bound 减去 lower_bound 就是等于 x 的数量
¶ set/map 上的查找
set<int> ss.lower_bound(x)返回迭代器s.upper_bound(x)返回迭代器s.find(x)返回迭代器s.count(x)返回 0/1
上述方法会用容器底层实现的特性实现查找,如果直接用 lower_bound(a.begin(), a.end(), x) 会得到非最优的时间复杂度。
¶ 实数二分
#include <bits/stdc++.h>
using namespace std;
double f(double x)
{
return 114 * x * x * x - 514 * x * x + 1919 * x - 810;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
double eps = 1e-12;
double l = 0; // f(l) < 0
double r = 1; // f(r) > 0
while (r - l > eps)
{
double mid = (l + r) / 2;
if (f(mid) < 0)
l = mid;
else
r = mid;
}
cout << fixed << setprecision(10) << l << "\n";
return 0;
}
¶ 二分答案
当可行解堆积在答案区间的某一侧,需要求解可行解与不可行解的交界点时,可以采用二分答案的方式处理。
一般来说都是一些:“正面求解答案”很困难,但是“验证某个答案是否合法”很简单,的题目中。
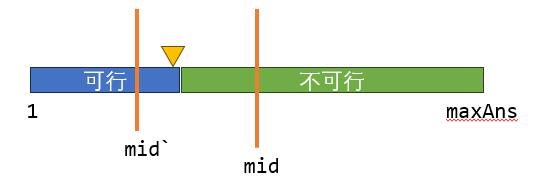
int l = ...;
int r = ...;
int ans = -1;
while (l <= r)
{
int mid = (l + r) / 2;
if (check(mid))
{
ans = mid;
l = mid + 1;
}
else
r = mid - 1;
}
cout << ans << "\n";
¶ 三分
const double eps = 1e-12;
double l = 0;
double r = 20;
while (r - l > eps)
{
double L = (l + r) / 2;
double R = (L + r) / 2;
if (f(L) < f(R))
r = R;
else
l = L;
}
cout << fixed << setprecision(10) << f(l);