¶ 前置知识
¶ 啥
¶ 字典树
简单来说就是在字典树上做字符串匹配。基础的字典树有下面这些内容:
int tr[MAXN + 5][26], tot; //根节点为 0
int cnt[MAXN + 5];
void insert(string &s)
{
int u = 0;
// cout << u;
for (int i = 0; i < s.length(); i++)
{
// cout << " -> " << s[i];
if (!tr[u][s[i] - 'a'])
tr[u][s[i] - 'a'] = ++tot;
u = tr[u][s[i] - 'a'];
}
cnt[u]++;
// cout << " cnt:" << cnt[u] << endl;
}
字典树上的每个节点都表示了某个字符串的某个前缀。
¶ 失配指针
AC 自动机时在这个基础上给每个节点都配置了一个失配指针。
int fail[MAXN + 5];
失配指针的含义是 root~fail[u] 对应的单词(显然是字典树中某个字符串的前缀)是 root~u 对应的单词的后缀,且是最长的那个。
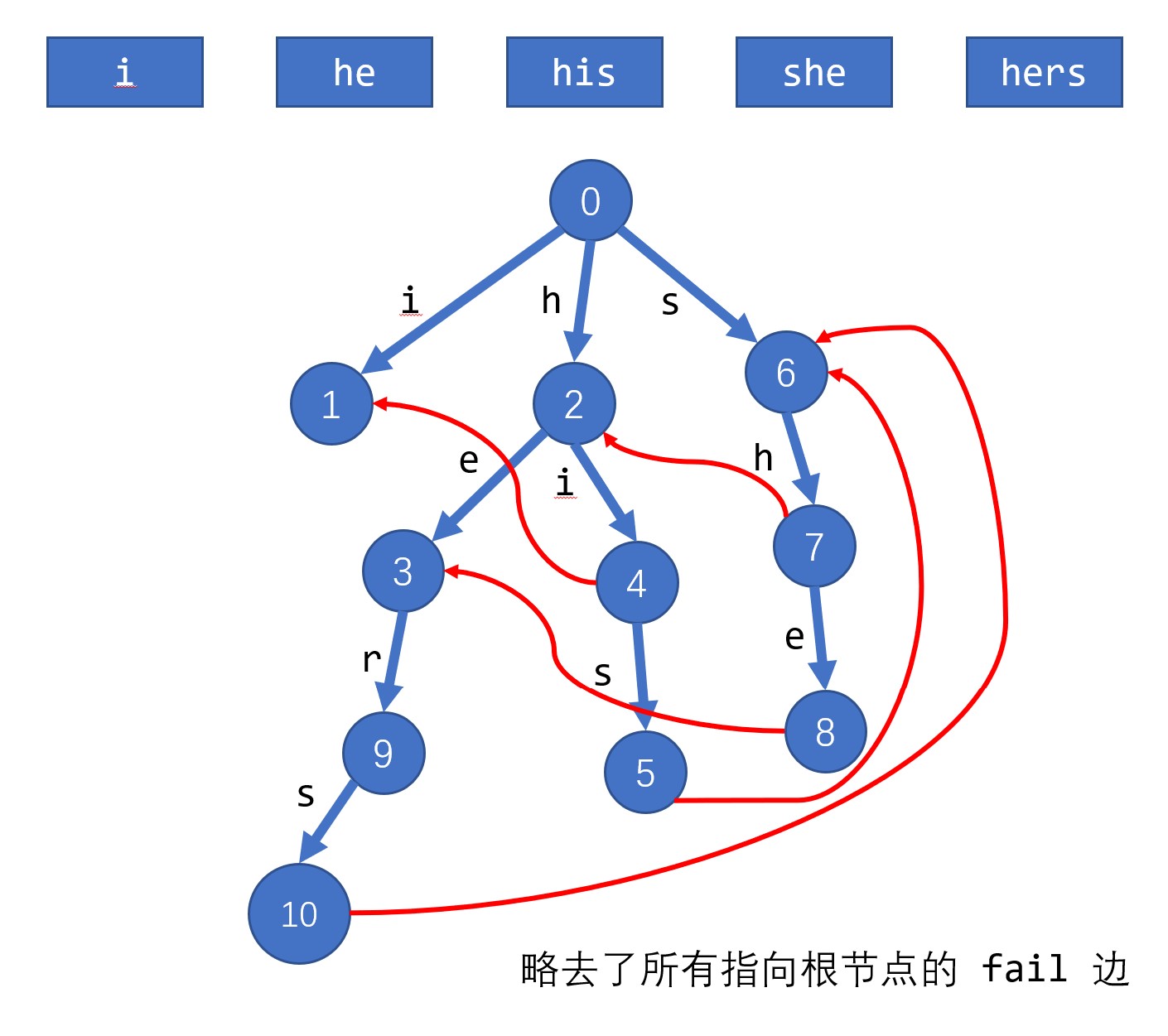
¶ 多模式匹配
这样我们就可以很方便地进行多模式匹配了,比如在上图这个例子中,如果我们需要看看 shishe 这个字符串里面能匹配 i,he,his,she,hers 中的哪些单词时:
s|hishe:6号点sh|ishe:7号点sh|ishe:2号点7号点下面没有i这条边了,发生了失配,所以我们需要跳fail[7]边到2号点来找i
shi|she:4号点shis|he:5号点shis|he:6号点5号点下面没有h这条边了,发生了失配,所以我们需要跳fail[5]边到6号点来找h
shish|e:7号点shishe|:8号点
显然走到 4 号点时,不光说明匹配上了 hi 还说明匹配上了 i。走到 8 号点时不光说明匹配上了 she 还说明匹配上了 he。所以走到每个点时都可以跳一下 fail 树来找到一次结尾匹配上了多少条边。
¶ 构造失配指针
假设当前做到了点 u,它在字典树上有一个子节点 v(边对应的字母为 'v')。
根据定义我们要求 root~fail[v] 是 root~v 的最长后缀。那么显然 root~fa[fail[v]] 是 root~u 的一个后缀。
从 u 不停跳 fail 边(for(int j=u;...;j=fail[j])),即可得到字典树中 root~u 的所有后缀,那么在这个过程中如果存在某个 j 存在 'v' 边,那么 fail[v] 就是 tr[j]['v'] 。
实际的代码中,匹配到点 u 后,如果下面要找 'v' 边,但不存在 'v' 边(失配了的时候),就会看 fail[u],尝试走到 tr[fail[u]]['v']。
所以不妨直接就把 tr[u]['v'] 设置为 tr[fail[u]]['v']。这样最后匹配时就能直接往下走了,并且整个图所有节点的所有子边就都有了。(这样连接完后的字典树被称为字典图)
//build()
for (int i = 0; i < 26; i++)
if (tr[0][i])
q.push(tr[0][i]);
while (!q.empty())
{
int u = q.front();
q.pop();
for (int i = 0; i < 26; i++)
{
if (tr[u][i])
{
fail[tr[u][i]] = tr[fail[u]][i];
q.push(tr[u][i]);
}
else
tr[u][i] = tr[fail[u]][i];
}
}
¶ 模板
¶ P3808 【模板】AC 自动机(简单版)
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1123456;
int n;
struct AC
{
int tr[MAXN][26], tot; //根节点为 0
int cnt[MAXN], fail[MAXN];
void insert(string &s)
{
int u = 0;
// cout << u;
for (int i = 0; i < s.length(); i++)
{
// cout << " -> " << s[i];
if (!tr[u][s[i] - 'a'])
tr[u][s[i] - 'a'] = ++tot;
u = tr[u][s[i] - 'a'];
}
cnt[u]++;
// cout << " cnt:" << cnt[u] << endl;
}
queue<int> q;
void build()
{
for (int i = 0; i < 26; i++)
if (tr[0][i])
q.push(tr[0][i]);
while (!q.empty())
{
int u = q.front();
q.pop();
for (int i = 0; i < 26; i++)
{
if (tr[u][i])
{
fail[tr[u][i]] = tr[fail[u]][i];
q.push(tr[u][i]);
}
else
tr[u][i] = tr[fail[u]][i];
}
}
}
int query(string &s)
{
int res = 0;
int u = 0;
for (int i = 0; i < s.length(); i++)
{
u = tr[u][s[i] - 'a'];
for (int j = u; j != 0 && cnt[j] != -1; j = fail[j])
{
res += cnt[j];
cnt[j] = -1;
}
}
return res;
}
};
AC ac;
string s;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> s;
ac.insert(s);
}
ac.build();
cin >> s;
cout << ac.query(s) << endl;
return 0;
}
¶ P3796 【模板】AC 自动机(加强版)
#include <bits/stdc++.h>
using namespace std;
const int MAXT = 50 + 5;
const int MAXN = 150 + 5;
int T, n;
string s[MAXT][MAXN], t;
int scnt[MAXT][MAXN];
struct AC
{
int tr[MAXN * 70 + 5][26], tot; //根节点为 0
int cnt[MAXN * 70 + 5], fail[MAXN * 70 + 5], idx[MAXN * 70 + 5];
void insert(string &s, int id)
{
int u = 0;
// cout << u;
for (int i = 0; i < s.length(); i++)
{
// cout << " -> " << s[i];
if (!tr[u][s[i] - 'a'])
tr[u][s[i] - 'a'] = ++tot;
u = tr[u][s[i] - 'a'];
}
idx[u] = id;
// cout << " cnt:" << cnt[u] << endl;
}
queue<int> q;
void build()
{
for (int i = 0; i < 26; i++)
if (tr[0][i])
q.push(tr[0][i]);
while (!q.empty())
{
int u = q.front();
q.pop();
for (int i = 0; i < 26; i++)
{
if (tr[u][i])
{
fail[tr[u][i]] = tr[fail[u]][i];
q.push(tr[u][i]);
}
else
tr[u][i] = tr[fail[u]][i];
}
}
}
int query(string &s)
{
int res = 0;
int u = 0;
for (int i = 0; i < s.length(); i++)
{
u = tr[u][s[i] - 'a'];
for (int j = u; j != 0 && cnt[j] != -1; j = fail[j])
cnt[j]++;
}
for (int i = 0; i <= tot; i++)
if (idx[i])
res = max(res, cnt[i]), scnt[T][idx[i]] = cnt[i];
return res;
}
};
AC ac[MAXT];
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
while (cin >> n)
{
if (n == 0)
break;
T++;
for (int i = 1; i <= n; i++)
{
cin >> s[T][i];
ac[T].insert(s[T][i], i);
}
ac[T].build();
cin >> t;
int ans = ac[T].query(t);
cout << ans << "\n";
for (int i = 1; i <= n; i++)
if (scnt[T][i] == ans)
cout << s[T][i] << "\n";
}
return 0;
}
¶ P5357 【模板】AC 自动机(二次加强版)
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 212345;
int n;
struct AC
{
int tr[MAXN][26], tot; // 根节点为 0
int cnt[MAXN], fail[MAXN];
int idx[MAXN]; // 每个模式串对应的终点坐标
// fail树相关
int inD[MAXN];
void insert(string &s, int id)
{
int u = 0;
// cout << u;
for (int i = 0; i < s.length(); i++)
{
// cout << " -> " << s[i];
if (!tr[u][s[i] - 'a'])
tr[u][s[i] - 'a'] = ++tot;
u = tr[u][s[i] - 'a'];
}
idx[id] = u;
// cnt[u]++;
// cout << " cnt:" << cnt[u] << endl;
}
queue<int> q;
void build()
{
for (int i = 0; i < 26; i++)
if (tr[0][i])
q.push(tr[0][i]);
while (!q.empty())
{
int u = q.front();
q.pop();
for (int i = 0; i < 26; i++)
{
if (tr[u][i])
{
fail[tr[u][i]] = tr[fail[u]][i];
inD[tr[fail[u]][i]]++;
q.push(tr[u][i]);
}
else
tr[u][i] = tr[fail[u]][i];
}
}
}
bool vis[MAXN];
void query(string &s)
{
int u = 0;
for (int i = 0; i < s.length(); i++)
{
u = tr[u][s[i] - 'a'];
cnt[u]++;
}
queue<int> q;
for (int i = 0; i <= tot; i++)
if (inD[i] == 0)
q.push(i), vis[i] = true;
while (!q.empty())
{
int now = q.front();
q.pop();
int nxt = fail[now];
inD[nxt]--;
cnt[nxt] += cnt[now];
if (inD[nxt] == 0 && !vis[nxt])
q.push(nxt), vis[nxt] = true;
}
}
};
AC ac;
string s;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> s;
ac.insert(s, i);
}
ac.build();
cin >> s;
ac.query(s);
/*
for (int i = 0; i <= ac.tot; i++)
{
cout << i << ": ";
for (int j = 0; j <= 1; j++)
cout << ac.tr[i][j] << " ";
cout << ", " << ac.fail[i] << "\n";
}
*/
for (int i = 1; i <= n; i++)
cout << ac.cnt[ac.idx[i]] << "\n"; //<< " " << ac.idx[i]
return 0;
}